What Is a Major in College and Why It Is Important?


P(E) = 0 if and only if E is an impossible event. These solutions will help you with a deeper knowledge of the basic concepts of Probability, thereby, making it a hassle-free learning experience for all students.
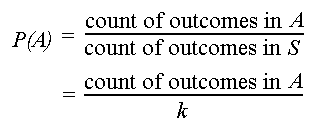
3.

Probability is a branch of math which deals with finding out the likelihood of the occurrence of an event. The result of an event after experimenting with the side of the coin after flipping, the number appearing on dice after rolling and a card is drawn out from a pack of well-shuffled cards, etc. It has several applications in the advanced concepts of mathematics and statistics. Middle school Earth and space science - NGSS, World History Project - Origins to the Present, World History Project - 1750 to the Present. Answer: Therefore the probability of picking a prime number and a prime number again is 6/25. The three types of probabilities are theoretical probability, experimental probability, and axiomatic probability. 2. where, \(\begin{align}P(A|B) \end{align}\) denotes how often event A happens on a condition that B happens.

The smallest possible probability is zero, and the largest is one. A Poisson distribution is for events such as antigen detection in a plasma sample, where the probabilities are numerous. Example 2: In a bag, there are 6 blue balls and 8 yellow balls.

Probability has huge applications in games and analysis. There are applications of permutation and combinations in some sums of Probability, as well. An event can be defined as a subset of sample space. This formula is going to help you to get the probability of any particular event.


Square Formula - All Formula of Square, Derivation and Solved Examples, Combination Formula in Maths | Combination Formula - Examples & Derivation, Area of a Sector of a Circle Formula - Solved Questions & Examples, Perimeter of a Trapezoid Formula |Trapezoid Area Formula - Derivation & Examples, Terminologies Related to Probability Formula. This indicates that besides this there is no chance that any other result will come. If you're seeing this message, it means we're having trouble loading external resources on our website. n(S) is the total number of events occurring in a sample space. Probability of non-occurrence of the same event is P(A). The probability can be determined by first knowing the sample space of outcomes of an experiment. The combination of all possible outcomes of an experiment like getting head or tail on a tossed coin, getting an even or odd number on dice, etc.


Further, the word probable in the legal content was referred to a proposition that had tangible proof. The experimental probability gives a realistic value and is based on the experimental values for calculation. 5/6 = 1/5 (or 20%) chance that you will actually roll a three on the first try, What Are Financial Projections? To get 10, we can have three favorable outcomes. For example: let us consider that two events are taking place namely A and B. \(P(A_1) + P(A_2) + P(A_3) + .P(A_n) = 1\).

Breakdown tough concepts through simple visuals. A random experiment cannot predict the exact outcomes but only some probable outcomes.

Sample Space: The set of all possible results or outcomes. Further, the new technology field of artificial intelligence is extensively based on probability. And the axiomatic probability is based on the axioms which govern the concepts of probability. P(face card) = 12/52 Thus we use the product of the probability of the events. Example 1: What is the probability of getting a sum of 10 when two dice are thrown?

This indicates that besides this there is no chance that any other result will come. where, \(\begin{align}P(B|A) \end{align}\) denotes how often event B happens on a condition that A happens. Any particular situation or an event for which we are required to find the probability is known as an experiment.

It is very important to have a clear understanding of the mathematical applications of these above formulas, to solve the sums of this topic. The two important probability distributions are binomial distribution and Poisson distribution. Number of face cards = Favorable outcomes = 12 The binomial distribution is defined for events with two probability outcomes and for events with a multiple number of times of such events. If there are two events A and B, conditional probability is a chance of occurrence of event B provided the event A has already occurred. Sample Space= (1,1),(1,2),(1,3),(1,4),(1,5),(1,6)(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)(6,1),(6,2),(6,3),(6,4),(6,5),(6,6){(1, 1), (1, 2), (1,3), (1,4), (1,5), (1, 6)} {(2, 1), (2, 2),(2,3), (2,4), (2,5), (2, 6)} {(3, 1), (3, 2), (3,3), (3,4), (3,5), (3, 6)} {(4, 1), (4, 2), (4,3), (4,4), (4,5), (4, 6)} {(5, 1), (5,2), (5,3), (5,4), (5,5), (5, 6)} {(6, 1), (6, 2), (6,3), (6,4), (6,5), (6, 6)} n(S) = 36, Favourable outcomes = {(1, 5), (2, 4), (3, 3), (4, 2) and (5, 1)}, P(Getting sum of numbers on two dice 6) = 5/ 36. The set of all possible results or outcomes. Probability is that branch of mathematics that is concerned with the numerical description of how likely there are chances of the event to occur or how likely a particular proposition is true. \(\begin{align}P(A) \end{align}\) the likelihood of occurrence of event A. Rolling a dice, tossing a coin are the most simple examples we can use. Khan Academy is a 501(c)(3) nonprofit organization. The Poisson distribution is based on the numerous probability outcomes in a limited space of time, distance, sample space. To Calculate the probability of an event to occur we use this probability formula, recalling, the probability is the likelihood of an event to happen.

You can find very good study resources for the topic of Probability on Vedantu, for both 10th and 12th-grade syllabi. The topic of Probability carries a considerable weightage in both Class 10 and Class 12 Mathematics examinations. 48 Motivational Career Quotes To Help You Find Success, Inbound Marketing vs. It is expressed as, Probability of an event P(E) = (Number of favorable outcomes) (Sample space). The field of permutations and combinations, statistical inference, cryptoanalysis, frequency analysis have altogether contributed to this current field of probability. Probability = (Favorable Outcomes)(Total Favourable Outcomes) The following activities in our real-life tend to follow the probability formula: The conditional probability depends upon the happening of one event based on the happening of another event.

No. Pulling out the exact matching socks of the same color. Rolling a dice, tossing a coin are the most simple examples we can use. You must have heard the term probability being coined for predicting the weather forecast in news TV bulletins for the next few days for some parts of the country. The formula for the conditional probability of happening of event B, given that event A, has happened is P(B/A) = P(A B)/P(A). Requirements To Be A Senator (With Steps, Skills and Salary), How To Choose a Type of Budget in 5 Easy Steps, 4 Content Syndication Strategies (With Benefits and Tips), How To Create a PTO Policy (And Pros and Cons). The experimental probability is based on the results and the values obtained from the probability experiments. These solutions are prepared by the subject matter experts at Vedantu, in strict adherence to the CBSE guidelines. The use of the word probable started first in the seventeenth century when it was referred to actions or opinions which were held by sensible people. 0 indicates the impossibility of the event to happen while 1 indicates certainty that the event is certain to occur.

Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event. m = 3/13, Answer: The probability of getting a face card is 3/13, go to slidego to slidego to slidego to slide. Probability is one of the most interesting topics covered in school level mathematics. If the probability of occurring an event is P(A) then the probability of not occurring an event is. Example 4: Find the probability of getting a face card from a standard deck of cards using the probability formula.

Event: The combination of all possible outcomes of an experiment like getting head or tail on a tossed coin, getting an even or odd number on dice, etc.




Chances of winning or losing in any sports. What are the common formulas used in probability sums? Using Probability Formula, Example 3: There are 5 cards numbered: 2, 3, 4, 5, 6. Solution: To find: You will commonly find sums on rolling of dice, tossing a pair of coins, pack of cards, drawing of different coloured balls or marbles from a bag, etc, from the topic of Probability. The probability calculates the happening of an experiment and it calculates the happening of a particular event with respect to the entire set of events. Experiment: Any particular situation or an event for which we are required to find the probability is known as an experiment. You just need to have the events for which you are looking for the probability and the formulas are going to make your work easier. The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes). After having a look at the solved papers and examples, students should go with understanding the basics of probability. Let us check the below points, which help us summarize the key learnings for this topic of probability. For helping the students many mock tests are available at Vedantu that will help the students to get a better knowledge of this topic. The probability of an event happening is obtained by dividing the number of outcomes of an event by the total number of possible outcomes or sample space. Where can I find good study resources for the topic of probability? If there are n number of events in an experiment, then the sum of the probabilities of those n events is always equal to 1. Find the probability of getting a blue ball.

Our mission is to provide a free, world-class education to anyone, anywhere. Some of the formulas that are commonly used in these sums are as follows. The conditional probability formula of happening of event B, given that event A, has already happened is expressed as P(B/A) = P(A B)/P(A). The results of the experimental probability are based on real-life instances and may differ in values from theoretical probability. Is probability a difficult topic in maths? For simple events of a few numbers of events, it is easy to calculate the probability. An example of the binomial distribution is the tossing of a coin with two outcomes, and for conducting such a tossing experiment with n number of coins. 5. This concept seems to be a little different from the rest of the topics covered in the syllabus for Class 10 and 12 maths, but with good practice, students can easily master its applications. Find the probability of picking a prime number, and putting it back, you pick a composite number.

Yes, you can download the important notes for the Probability Formula free of cost from Vedantu.

It is an added advantage if you have a good concept of set theory, to understand the sums of Probability. Let us assume the probability of drawing a blue ball to be P(B), Number of favorable outcomes to get a blue ball = 6, P(B) = Number of favorable outcomes/Total number of outcomes = 6/14 = 3/7. Quite often the theoretical and experimental probability differ in their results. \(\begin{align}P(B) \end{align}\) the likelihood of occurrence of event B. The function helps in obtaining the probability of every outcome.


Hence you can refer to the stepwise solutions for a better understanding of the concept of Probability. (And How To Use Them), Types of Probability: Definition and Examples, How To Calculate Probability in Excel (With an Example), How To Calculate Combination Probability (Plus Examples), 6433 Champion Grandview Way Building 1, Austin, TX 78750, Probability differs from determining the odds. Probability of occurrence of an event is P(A). Content Marketing: Key Differences, How To Do Instagram Live Effectively: A Step-by-Step Guide, Visual Project Management: Definition and How To Use It, How To Reduce Your Bounce Rate and Why It's Important. Whatever the result is, it is from this sample Space only. There are NCERT solutions from the topic probability available on our website and mobile application. For calculating the probability of different types of situations, the probability formula and its related basic concepts are used. Probability is represented as a fraction and always lies between 0 and 1.
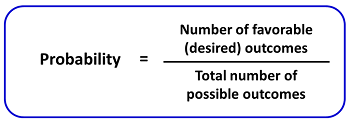
In the formulas given below, we are taking 2 events namely A and B. P(A)} {P(B)}\end{align}\). Calculate the probability of getting the sum of the numbers on the two dice is 6. An event that is certain has a probability equal to one. These notes are available on our webpage and you can also download the NCERT solutions for Probability from our mobile application or website for free. One ball is selected randomly from the bag. The two events are independent. Donate or volunteer today! Probability of getting a face card In general, the probability is the ratio of the number of favorable outcomes to the total outcomes in that sample space.

Math will no longer be a tough subject, especially when you understand the concepts through visualizations. Then they should look out for the formulas and other examples that Vedantu provides you side by side so that you are well aware of the application of the concept that you have studied.

The desired outcome is 10. The outcome of throwing a coin is a head or a tail and the outcome of throwing dice is 1, 2, 3, 4, 5, or 6. P(H) = Number of heads/Total outcomes = 1/2, P(T)= Number of Tails/ Total outcomes = 1/2, P(2H) = P(0 T) = Number of outcome with two heads/Total Outcomes = 1/4, P(1H) = P(1T) = Number of outcomes with only one head/Total Outcomes = 2/4 = 1/2, P(0H) = (2T) = Number of outcome with two heads/Total Outcomes = 1/4, P(0H) = P(3T) = Number of outcomes with no heads/Total Outcomes = 1/8, P(1H) = P(2T) = Number of Outcomes with one head/Total Outcomes = 3/8, P(2H) = P(1T) = Number of outcomes with two heads /Total Outcomes = 3/8, P(3H) = P(0T) = Number of outcomes with three heads/Total Outcomes = 1/8, P(Even Number) = Number of even number outcomes/Total Outcomes = 3/6 = 1/2, P(Odd Number) = Number of odd number outcomes/Total Outcomes = 3/6 = 1/2, P(Prime Number) = Number of prime number outcomes/Total Outcomes = 3/6 = 1/2, Probability of getting a doublet(Same number) = 6/36 = 1/6, Probability of getting a number 3 on at least one dice = 11/36, Probability of getting a sum of 7 = 6/36 = 1/6, The probability of drawing a black card is P(Black card) = 26/52 = 1/2, The probability of drawing a hearts card is P(Hearts) = 13/52 = 1/4, The probability of drawing a face card is P(Face card) = 12/52 = 3/13, The probability of drawing a card numbered 4 is P(4) = 4/52 = 1/13, The probability of drawing a red card numbered 4 is P(4 Red) = 2/52 = 1/26. Probability is a measure of how likely an event is to happen. Explore what probability means and why it's useful. 1.

Two dice are rolled simultaneously. Also in real life and industry areas where it is about prediction we make use of probability. Given: Total number of cards = 52

Probability is the way to measure the uncertainty, how likely an event has happened or is bound to happen. There are 36 possibilities when we throw two dice. P(getting a prime) = n(favorable events)/ n(sample space) = {2, 3, 5}/{2, 3, 4, 5, 6} = 3/5, p(getting a composite) = n(favorable events)/ n(sample space) = {4, 6}/{2, 3, 4, 5, 6}= 2/5, Thus the total probability of the two independent events= P(prime) P(composite). Probability of obtaining an odd number on rolling dice for once. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. There are a few formulas that students need to learn and practice to develop a good understanding of the concepts and applications of Probability.

What is the easiest way by which students can understand probability? Whatever the result is, it is from this sample Space only. To understand the probability concepts easily, first, the students need to go through the solved question papers and the examples of probability. The value of probability ranges between 0 and 1, where 0 denotes uncertainty and 1 denotes certainty. P(E) = 1 if and only if E is a certain event. Probability measures the chance of an event happening and is equal to the number of favorable events divided by the total number of events.


The conditional probability predicts the happening of one event based on the happening of another event. Probability of an event = number of favorable outcomes/ sample space, Probability of getting number 10 = 3/36 =1/12. Calculate the probability of getting the sum of the numbers on the two dice is 6. Answer: Therefore the probability of getting a sum of 10 is 1/12. Answer: Therefore the probability of drawing a blue ball is 3/7. A probability is generally calculated for an event (x) within the sample space. The probability of any event depends upon the number of favorable outcomes and the total outcomes. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked. Any two mutually exclusive events cannot occur simultaneously, while the union of events says only one of them can occur. Probability Function: The function helps in obtaining the probability of every outcome. The prediction of the price of a stock, or the performance of a team in cricket requires the use of probability concepts. Outcome: The result of an event after experimenting with the side of the coin after flipping, the number appearing on dice after rolling and a card is drawn out from a pack of well-shuffled cards, etc. For any event the probability lies between 0 to 1. Example 01: Probability of obtaining an odd number on rolling dice for once. So for the probability that event A can happen, we are going to write P(A) and for the probability that event B can happen, we can write P(B). CBSE Previous Year Question Paper for Class 10, CBSE Previous Year Question Paper for Class 12. The theoretical probability calculates the probability based on formulas and input values. The formulas are based on these events only. Experimental probability is defined as the ratio of the total number of times an event has occurred to the total number of trials conducted. Solution: Sample Space = {1, 2, 3, 4, 5, 6}, P(Getting an odd number) = 3 / 6 = = 0.5. Some probability important formulas based on them are as follows: Example 01: Two dice are rolled simultaneously. Ph.D. vs. Master's Degree: What's the Difference? Statistics helps in rightly analyzing. Can I download the important notes on probability formula for free? 4. But for calculating probabilities involving numerous events and to manage huge data relating to those events we need the help of statistics. There are a few crucial terminologies that are associated with all probability formulas. n(B) is the number of favorable outcomes of an event 'B'. This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.

 P(E) = 0 if and only if E is an impossible event. These solutions will help you with a deeper knowledge of the basic concepts of Probability, thereby, making it a hassle-free learning experience for all students.
P(E) = 0 if and only if E is an impossible event. These solutions will help you with a deeper knowledge of the basic concepts of Probability, thereby, making it a hassle-free learning experience for all students. 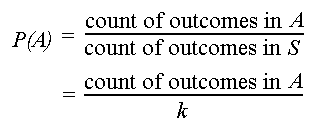 3.
3.  Probability is a branch of math which deals with finding out the likelihood of the occurrence of an event. The result of an event after experimenting with the side of the coin after flipping, the number appearing on dice after rolling and a card is drawn out from a pack of well-shuffled cards, etc. It has several applications in the advanced concepts of mathematics and statistics. Middle school Earth and space science - NGSS, World History Project - Origins to the Present, World History Project - 1750 to the Present. Answer: Therefore the probability of picking a prime number and a prime number again is 6/25. The three types of probabilities are theoretical probability, experimental probability, and axiomatic probability. 2. where, \(\begin{align}P(A|B) \end{align}\) denotes how often event A happens on a condition that B happens.
Probability is a branch of math which deals with finding out the likelihood of the occurrence of an event. The result of an event after experimenting with the side of the coin after flipping, the number appearing on dice after rolling and a card is drawn out from a pack of well-shuffled cards, etc. It has several applications in the advanced concepts of mathematics and statistics. Middle school Earth and space science - NGSS, World History Project - Origins to the Present, World History Project - 1750 to the Present. Answer: Therefore the probability of picking a prime number and a prime number again is 6/25. The three types of probabilities are theoretical probability, experimental probability, and axiomatic probability. 2. where, \(\begin{align}P(A|B) \end{align}\) denotes how often event A happens on a condition that B happens.  The smallest possible probability is zero, and the largest is one. A Poisson distribution is for events such as antigen detection in a plasma sample, where the probabilities are numerous. Example 2: In a bag, there are 6 blue balls and 8 yellow balls.
The smallest possible probability is zero, and the largest is one. A Poisson distribution is for events such as antigen detection in a plasma sample, where the probabilities are numerous. Example 2: In a bag, there are 6 blue balls and 8 yellow balls.  Probability has huge applications in games and analysis. There are applications of permutation and combinations in some sums of Probability, as well. An event can be defined as a subset of sample space. This formula is going to help you to get the probability of any particular event.
Probability has huge applications in games and analysis. There are applications of permutation and combinations in some sums of Probability, as well. An event can be defined as a subset of sample space. This formula is going to help you to get the probability of any particular event. 
 Square Formula - All Formula of Square, Derivation and Solved Examples, Combination Formula in Maths | Combination Formula - Examples & Derivation, Area of a Sector of a Circle Formula - Solved Questions & Examples, Perimeter of a Trapezoid Formula |Trapezoid Area Formula - Derivation & Examples, Terminologies Related to Probability Formula. This indicates that besides this there is no chance that any other result will come. If you're seeing this message, it means we're having trouble loading external resources on our website. n(S) is the total number of events occurring in a sample space. Probability of non-occurrence of the same event is P(A). The probability can be determined by first knowing the sample space of outcomes of an experiment. The combination of all possible outcomes of an experiment like getting head or tail on a tossed coin, getting an even or odd number on dice, etc.
Square Formula - All Formula of Square, Derivation and Solved Examples, Combination Formula in Maths | Combination Formula - Examples & Derivation, Area of a Sector of a Circle Formula - Solved Questions & Examples, Perimeter of a Trapezoid Formula |Trapezoid Area Formula - Derivation & Examples, Terminologies Related to Probability Formula. This indicates that besides this there is no chance that any other result will come. If you're seeing this message, it means we're having trouble loading external resources on our website. n(S) is the total number of events occurring in a sample space. Probability of non-occurrence of the same event is P(A). The probability can be determined by first knowing the sample space of outcomes of an experiment. The combination of all possible outcomes of an experiment like getting head or tail on a tossed coin, getting an even or odd number on dice, etc. 
 Further, the word probable in the legal content was referred to a proposition that had tangible proof. The experimental probability gives a realistic value and is based on the experimental values for calculation. 5/6 = 1/5 (or 20%) chance that you will actually roll a three on the first try, What Are Financial Projections? To get 10, we can have three favorable outcomes. For example: let us consider that two events are taking place namely A and B. \(P(A_1) + P(A_2) + P(A_3) + .P(A_n) = 1\).
Further, the word probable in the legal content was referred to a proposition that had tangible proof. The experimental probability gives a realistic value and is based on the experimental values for calculation. 5/6 = 1/5 (or 20%) chance that you will actually roll a three on the first try, What Are Financial Projections? To get 10, we can have three favorable outcomes. For example: let us consider that two events are taking place namely A and B. \(P(A_1) + P(A_2) + P(A_3) + .P(A_n) = 1\).  Breakdown tough concepts through simple visuals. A random experiment cannot predict the exact outcomes but only some probable outcomes.
Breakdown tough concepts through simple visuals. A random experiment cannot predict the exact outcomes but only some probable outcomes.  Sample Space: The set of all possible results or outcomes. Further, the new technology field of artificial intelligence is extensively based on probability. And the axiomatic probability is based on the axioms which govern the concepts of probability. P(face card) = 12/52 Thus we use the product of the probability of the events. Example 1: What is the probability of getting a sum of 10 when two dice are thrown?
Sample Space: The set of all possible results or outcomes. Further, the new technology field of artificial intelligence is extensively based on probability. And the axiomatic probability is based on the axioms which govern the concepts of probability. P(face card) = 12/52 Thus we use the product of the probability of the events. Example 1: What is the probability of getting a sum of 10 when two dice are thrown?  This indicates that besides this there is no chance that any other result will come. where, \(\begin{align}P(B|A) \end{align}\) denotes how often event B happens on a condition that A happens. Any particular situation or an event for which we are required to find the probability is known as an experiment.
This indicates that besides this there is no chance that any other result will come. where, \(\begin{align}P(B|A) \end{align}\) denotes how often event B happens on a condition that A happens. Any particular situation or an event for which we are required to find the probability is known as an experiment.  It is very important to have a clear understanding of the mathematical applications of these above formulas, to solve the sums of this topic. The two important probability distributions are binomial distribution and Poisson distribution. Number of face cards = Favorable outcomes = 12 The binomial distribution is defined for events with two probability outcomes and for events with a multiple number of times of such events. If there are two events A and B, conditional probability is a chance of occurrence of event B provided the event A has already occurred. Sample Space= (1,1),(1,2),(1,3),(1,4),(1,5),(1,6)(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)(6,1),(6,2),(6,3),(6,4),(6,5),(6,6){(1, 1), (1, 2), (1,3), (1,4), (1,5), (1, 6)} {(2, 1), (2, 2),(2,3), (2,4), (2,5), (2, 6)} {(3, 1), (3, 2), (3,3), (3,4), (3,5), (3, 6)} {(4, 1), (4, 2), (4,3), (4,4), (4,5), (4, 6)} {(5, 1), (5,2), (5,3), (5,4), (5,5), (5, 6)} {(6, 1), (6, 2), (6,3), (6,4), (6,5), (6, 6)} n(S) = 36, Favourable outcomes = {(1, 5), (2, 4), (3, 3), (4, 2) and (5, 1)}, P(Getting sum of numbers on two dice 6) = 5/ 36. The set of all possible results or outcomes. Probability is that branch of mathematics that is concerned with the numerical description of how likely there are chances of the event to occur or how likely a particular proposition is true. \(\begin{align}P(A) \end{align}\) the likelihood of occurrence of event A. Rolling a dice, tossing a coin are the most simple examples we can use. Khan Academy is a 501(c)(3) nonprofit organization. The Poisson distribution is based on the numerous probability outcomes in a limited space of time, distance, sample space. To Calculate the probability of an event to occur we use this probability formula, recalling, the probability is the likelihood of an event to happen.
It is very important to have a clear understanding of the mathematical applications of these above formulas, to solve the sums of this topic. The two important probability distributions are binomial distribution and Poisson distribution. Number of face cards = Favorable outcomes = 12 The binomial distribution is defined for events with two probability outcomes and for events with a multiple number of times of such events. If there are two events A and B, conditional probability is a chance of occurrence of event B provided the event A has already occurred. Sample Space= (1,1),(1,2),(1,3),(1,4),(1,5),(1,6)(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)(1,1),(1,2),(1,3),(1,4),(1,5),(1,6)(2,1),(2,2),(2,3),(2,4),(2,5),(2,6)(3,1),(3,2),(3,3),(3,4),(3,5),(3,6)(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)(5,1),(5,2),(5,3),(5,4),(5,5),(5,6)(6,1),(6,2),(6,3),(6,4),(6,5),(6,6){(1, 1), (1, 2), (1,3), (1,4), (1,5), (1, 6)} {(2, 1), (2, 2),(2,3), (2,4), (2,5), (2, 6)} {(3, 1), (3, 2), (3,3), (3,4), (3,5), (3, 6)} {(4, 1), (4, 2), (4,3), (4,4), (4,5), (4, 6)} {(5, 1), (5,2), (5,3), (5,4), (5,5), (5, 6)} {(6, 1), (6, 2), (6,3), (6,4), (6,5), (6, 6)} n(S) = 36, Favourable outcomes = {(1, 5), (2, 4), (3, 3), (4, 2) and (5, 1)}, P(Getting sum of numbers on two dice 6) = 5/ 36. The set of all possible results or outcomes. Probability is that branch of mathematics that is concerned with the numerical description of how likely there are chances of the event to occur or how likely a particular proposition is true. \(\begin{align}P(A) \end{align}\) the likelihood of occurrence of event A. Rolling a dice, tossing a coin are the most simple examples we can use. Khan Academy is a 501(c)(3) nonprofit organization. The Poisson distribution is based on the numerous probability outcomes in a limited space of time, distance, sample space. To Calculate the probability of an event to occur we use this probability formula, recalling, the probability is the likelihood of an event to happen.  You can find very good study resources for the topic of Probability on Vedantu, for both 10th and 12th-grade syllabi. The topic of Probability carries a considerable weightage in both Class 10 and Class 12 Mathematics examinations. 48 Motivational Career Quotes To Help You Find Success, Inbound Marketing vs. It is expressed as, Probability of an event P(E) = (Number of favorable outcomes) (Sample space). The field of permutations and combinations, statistical inference, cryptoanalysis, frequency analysis have altogether contributed to this current field of probability. Probability = (Favorable Outcomes)(Total Favourable Outcomes) The following activities in our real-life tend to follow the probability formula: The conditional probability depends upon the happening of one event based on the happening of another event.
You can find very good study resources for the topic of Probability on Vedantu, for both 10th and 12th-grade syllabi. The topic of Probability carries a considerable weightage in both Class 10 and Class 12 Mathematics examinations. 48 Motivational Career Quotes To Help You Find Success, Inbound Marketing vs. It is expressed as, Probability of an event P(E) = (Number of favorable outcomes) (Sample space). The field of permutations and combinations, statistical inference, cryptoanalysis, frequency analysis have altogether contributed to this current field of probability. Probability = (Favorable Outcomes)(Total Favourable Outcomes) The following activities in our real-life tend to follow the probability formula: The conditional probability depends upon the happening of one event based on the happening of another event.  No. Pulling out the exact matching socks of the same color. Rolling a dice, tossing a coin are the most simple examples we can use. You must have heard the term probability being coined for predicting the weather forecast in news TV bulletins for the next few days for some parts of the country. The formula for the conditional probability of happening of event B, given that event A, has happened is P(B/A) = P(A B)/P(A). Requirements To Be A Senator (With Steps, Skills and Salary), How To Choose a Type of Budget in 5 Easy Steps, 4 Content Syndication Strategies (With Benefits and Tips), How To Create a PTO Policy (And Pros and Cons). The experimental probability is based on the results and the values obtained from the probability experiments. These solutions are prepared by the subject matter experts at Vedantu, in strict adherence to the CBSE guidelines. The use of the word probable started first in the seventeenth century when it was referred to actions or opinions which were held by sensible people. 0 indicates the impossibility of the event to happen while 1 indicates certainty that the event is certain to occur.
No. Pulling out the exact matching socks of the same color. Rolling a dice, tossing a coin are the most simple examples we can use. You must have heard the term probability being coined for predicting the weather forecast in news TV bulletins for the next few days for some parts of the country. The formula for the conditional probability of happening of event B, given that event A, has happened is P(B/A) = P(A B)/P(A). Requirements To Be A Senator (With Steps, Skills and Salary), How To Choose a Type of Budget in 5 Easy Steps, 4 Content Syndication Strategies (With Benefits and Tips), How To Create a PTO Policy (And Pros and Cons). The experimental probability is based on the results and the values obtained from the probability experiments. These solutions are prepared by the subject matter experts at Vedantu, in strict adherence to the CBSE guidelines. The use of the word probable started first in the seventeenth century when it was referred to actions or opinions which were held by sensible people. 0 indicates the impossibility of the event to happen while 1 indicates certainty that the event is certain to occur.  Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event. m = 3/13, Answer: The probability of getting a face card is 3/13, go to slidego to slidego to slidego to slide. Probability is one of the most interesting topics covered in school level mathematics. If the probability of occurring an event is P(A) then the probability of not occurring an event is. Example 4: Find the probability of getting a face card from a standard deck of cards using the probability formula.
Here, P(A) means finding the probability of an event A, n(E) means the number of favourable outcomes of an event and n(S) means the set of all possible outcomes of an event. m = 3/13, Answer: The probability of getting a face card is 3/13, go to slidego to slidego to slidego to slide. Probability is one of the most interesting topics covered in school level mathematics. If the probability of occurring an event is P(A) then the probability of not occurring an event is. Example 4: Find the probability of getting a face card from a standard deck of cards using the probability formula.  Event: The combination of all possible outcomes of an experiment like getting head or tail on a tossed coin, getting an even or odd number on dice, etc.
Event: The combination of all possible outcomes of an experiment like getting head or tail on a tossed coin, getting an even or odd number on dice, etc. 


 Chances of winning or losing in any sports. What are the common formulas used in probability sums? Using Probability Formula, Example 3: There are 5 cards numbered: 2, 3, 4, 5, 6. Solution: To find: You will commonly find sums on rolling of dice, tossing a pair of coins, pack of cards, drawing of different coloured balls or marbles from a bag, etc, from the topic of Probability. The probability calculates the happening of an experiment and it calculates the happening of a particular event with respect to the entire set of events. Experiment: Any particular situation or an event for which we are required to find the probability is known as an experiment. You just need to have the events for which you are looking for the probability and the formulas are going to make your work easier. The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes). After having a look at the solved papers and examples, students should go with understanding the basics of probability. Let us check the below points, which help us summarize the key learnings for this topic of probability. For helping the students many mock tests are available at Vedantu that will help the students to get a better knowledge of this topic. The probability of an event happening is obtained by dividing the number of outcomes of an event by the total number of possible outcomes or sample space. Where can I find good study resources for the topic of probability? If there are n number of events in an experiment, then the sum of the probabilities of those n events is always equal to 1. Find the probability of getting a blue ball.
Chances of winning or losing in any sports. What are the common formulas used in probability sums? Using Probability Formula, Example 3: There are 5 cards numbered: 2, 3, 4, 5, 6. Solution: To find: You will commonly find sums on rolling of dice, tossing a pair of coins, pack of cards, drawing of different coloured balls or marbles from a bag, etc, from the topic of Probability. The probability calculates the happening of an experiment and it calculates the happening of a particular event with respect to the entire set of events. Experiment: Any particular situation or an event for which we are required to find the probability is known as an experiment. You just need to have the events for which you are looking for the probability and the formulas are going to make your work easier. The probability of an Event = (Number of favourable outcomes) / (Total number of possible outcomes). After having a look at the solved papers and examples, students should go with understanding the basics of probability. Let us check the below points, which help us summarize the key learnings for this topic of probability. For helping the students many mock tests are available at Vedantu that will help the students to get a better knowledge of this topic. The probability of an event happening is obtained by dividing the number of outcomes of an event by the total number of possible outcomes or sample space. Where can I find good study resources for the topic of probability? If there are n number of events in an experiment, then the sum of the probabilities of those n events is always equal to 1. Find the probability of getting a blue ball.  Yes, you can download the important notes for the Probability Formula free of cost from Vedantu.
Yes, you can download the important notes for the Probability Formula free of cost from Vedantu.  It is an added advantage if you have a good concept of set theory, to understand the sums of Probability. Let us assume the probability of drawing a blue ball to be P(B), Number of favorable outcomes to get a blue ball = 6, P(B) = Number of favorable outcomes/Total number of outcomes = 6/14 = 3/7. Quite often the theoretical and experimental probability differ in their results. \(\begin{align}P(B) \end{align}\) the likelihood of occurrence of event B. The function helps in obtaining the probability of every outcome.
It is an added advantage if you have a good concept of set theory, to understand the sums of Probability. Let us assume the probability of drawing a blue ball to be P(B), Number of favorable outcomes to get a blue ball = 6, P(B) = Number of favorable outcomes/Total number of outcomes = 6/14 = 3/7. Quite often the theoretical and experimental probability differ in their results. \(\begin{align}P(B) \end{align}\) the likelihood of occurrence of event B. The function helps in obtaining the probability of every outcome. 
 Hence you can refer to the stepwise solutions for a better understanding of the concept of Probability. (And How To Use Them), Types of Probability: Definition and Examples, How To Calculate Probability in Excel (With an Example), How To Calculate Combination Probability (Plus Examples), 6433 Champion Grandview Way Building 1, Austin, TX 78750, Probability differs from determining the odds. Probability of occurrence of an event is P(A). Content Marketing: Key Differences, How To Do Instagram Live Effectively: A Step-by-Step Guide, Visual Project Management: Definition and How To Use It, How To Reduce Your Bounce Rate and Why It's Important. Whatever the result is, it is from this sample Space only. There are NCERT solutions from the topic probability available on our website and mobile application. For calculating the probability of different types of situations, the probability formula and its related basic concepts are used. Probability is represented as a fraction and always lies between 0 and 1.
Hence you can refer to the stepwise solutions for a better understanding of the concept of Probability. (And How To Use Them), Types of Probability: Definition and Examples, How To Calculate Probability in Excel (With an Example), How To Calculate Combination Probability (Plus Examples), 6433 Champion Grandview Way Building 1, Austin, TX 78750, Probability differs from determining the odds. Probability of occurrence of an event is P(A). Content Marketing: Key Differences, How To Do Instagram Live Effectively: A Step-by-Step Guide, Visual Project Management: Definition and How To Use It, How To Reduce Your Bounce Rate and Why It's Important. Whatever the result is, it is from this sample Space only. There are NCERT solutions from the topic probability available on our website and mobile application. For calculating the probability of different types of situations, the probability formula and its related basic concepts are used. Probability is represented as a fraction and always lies between 0 and 1.  In the formulas given below, we are taking 2 events namely A and B. P(A)} {P(B)}\end{align}\). Calculate the probability of getting the sum of the numbers on the two dice is 6. An event that is certain has a probability equal to one. These notes are available on our webpage and you can also download the NCERT solutions for Probability from our mobile application or website for free. One ball is selected randomly from the bag. The two events are independent. Donate or volunteer today! Probability of getting a face card In general, the probability is the ratio of the number of favorable outcomes to the total outcomes in that sample space.
In the formulas given below, we are taking 2 events namely A and B. P(A)} {P(B)}\end{align}\). Calculate the probability of getting the sum of the numbers on the two dice is 6. An event that is certain has a probability equal to one. These notes are available on our webpage and you can also download the NCERT solutions for Probability from our mobile application or website for free. One ball is selected randomly from the bag. The two events are independent. Donate or volunteer today! Probability of getting a face card In general, the probability is the ratio of the number of favorable outcomes to the total outcomes in that sample space.  Math will no longer be a tough subject, especially when you understand the concepts through visualizations. Then they should look out for the formulas and other examples that Vedantu provides you side by side so that you are well aware of the application of the concept that you have studied.
Math will no longer be a tough subject, especially when you understand the concepts through visualizations. Then they should look out for the formulas and other examples that Vedantu provides you side by side so that you are well aware of the application of the concept that you have studied.  The desired outcome is 10. The outcome of throwing a coin is a head or a tail and the outcome of throwing dice is 1, 2, 3, 4, 5, or 6. P(H) = Number of heads/Total outcomes = 1/2, P(T)= Number of Tails/ Total outcomes = 1/2, P(2H) = P(0 T) = Number of outcome with two heads/Total Outcomes = 1/4, P(1H) = P(1T) = Number of outcomes with only one head/Total Outcomes = 2/4 = 1/2, P(0H) = (2T) = Number of outcome with two heads/Total Outcomes = 1/4, P(0H) = P(3T) = Number of outcomes with no heads/Total Outcomes = 1/8, P(1H) = P(2T) = Number of Outcomes with one head/Total Outcomes = 3/8, P(2H) = P(1T) = Number of outcomes with two heads /Total Outcomes = 3/8, P(3H) = P(0T) = Number of outcomes with three heads/Total Outcomes = 1/8, P(Even Number) = Number of even number outcomes/Total Outcomes = 3/6 = 1/2, P(Odd Number) = Number of odd number outcomes/Total Outcomes = 3/6 = 1/2, P(Prime Number) = Number of prime number outcomes/Total Outcomes = 3/6 = 1/2, Probability of getting a doublet(Same number) = 6/36 = 1/6, Probability of getting a number 3 on at least one dice = 11/36, Probability of getting a sum of 7 = 6/36 = 1/6, The probability of drawing a black card is P(Black card) = 26/52 = 1/2, The probability of drawing a hearts card is P(Hearts) = 13/52 = 1/4, The probability of drawing a face card is P(Face card) = 12/52 = 3/13, The probability of drawing a card numbered 4 is P(4) = 4/52 = 1/13, The probability of drawing a red card numbered 4 is P(4 Red) = 2/52 = 1/26. Probability is a measure of how likely an event is to happen. Explore what probability means and why it's useful. 1.
The desired outcome is 10. The outcome of throwing a coin is a head or a tail and the outcome of throwing dice is 1, 2, 3, 4, 5, or 6. P(H) = Number of heads/Total outcomes = 1/2, P(T)= Number of Tails/ Total outcomes = 1/2, P(2H) = P(0 T) = Number of outcome with two heads/Total Outcomes = 1/4, P(1H) = P(1T) = Number of outcomes with only one head/Total Outcomes = 2/4 = 1/2, P(0H) = (2T) = Number of outcome with two heads/Total Outcomes = 1/4, P(0H) = P(3T) = Number of outcomes with no heads/Total Outcomes = 1/8, P(1H) = P(2T) = Number of Outcomes with one head/Total Outcomes = 3/8, P(2H) = P(1T) = Number of outcomes with two heads /Total Outcomes = 3/8, P(3H) = P(0T) = Number of outcomes with three heads/Total Outcomes = 1/8, P(Even Number) = Number of even number outcomes/Total Outcomes = 3/6 = 1/2, P(Odd Number) = Number of odd number outcomes/Total Outcomes = 3/6 = 1/2, P(Prime Number) = Number of prime number outcomes/Total Outcomes = 3/6 = 1/2, Probability of getting a doublet(Same number) = 6/36 = 1/6, Probability of getting a number 3 on at least one dice = 11/36, Probability of getting a sum of 7 = 6/36 = 1/6, The probability of drawing a black card is P(Black card) = 26/52 = 1/2, The probability of drawing a hearts card is P(Hearts) = 13/52 = 1/4, The probability of drawing a face card is P(Face card) = 12/52 = 3/13, The probability of drawing a card numbered 4 is P(4) = 4/52 = 1/13, The probability of drawing a red card numbered 4 is P(4 Red) = 2/52 = 1/26. Probability is a measure of how likely an event is to happen. Explore what probability means and why it's useful. 1.  Two dice are rolled simultaneously. Also in real life and industry areas where it is about prediction we make use of probability. Given: Total number of cards = 52
Two dice are rolled simultaneously. Also in real life and industry areas where it is about prediction we make use of probability. Given: Total number of cards = 52  Probability is the way to measure the uncertainty, how likely an event has happened or is bound to happen. There are 36 possibilities when we throw two dice. P(getting a prime) = n(favorable events)/ n(sample space) = {2, 3, 5}/{2, 3, 4, 5, 6} = 3/5, p(getting a composite) = n(favorable events)/ n(sample space) = {4, 6}/{2, 3, 4, 5, 6}= 2/5, Thus the total probability of the two independent events= P(prime) P(composite). Probability of obtaining an odd number on rolling dice for once. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. There are a few formulas that students need to learn and practice to develop a good understanding of the concepts and applications of Probability.
Probability is the way to measure the uncertainty, how likely an event has happened or is bound to happen. There are 36 possibilities when we throw two dice. P(getting a prime) = n(favorable events)/ n(sample space) = {2, 3, 5}/{2, 3, 4, 5, 6} = 3/5, p(getting a composite) = n(favorable events)/ n(sample space) = {4, 6}/{2, 3, 4, 5, 6}= 2/5, Thus the total probability of the two independent events= P(prime) P(composite). Probability of obtaining an odd number on rolling dice for once. To log in and use all the features of Khan Academy, please enable JavaScript in your browser. There are a few formulas that students need to learn and practice to develop a good understanding of the concepts and applications of Probability.  What is the easiest way by which students can understand probability? Whatever the result is, it is from this sample Space only. To understand the probability concepts easily, first, the students need to go through the solved question papers and the examples of probability. The value of probability ranges between 0 and 1, where 0 denotes uncertainty and 1 denotes certainty. P(E) = 1 if and only if E is a certain event. Probability measures the chance of an event happening and is equal to the number of favorable events divided by the total number of events.
What is the easiest way by which students can understand probability? Whatever the result is, it is from this sample Space only. To understand the probability concepts easily, first, the students need to go through the solved question papers and the examples of probability. The value of probability ranges between 0 and 1, where 0 denotes uncertainty and 1 denotes certainty. P(E) = 1 if and only if E is a certain event. Probability measures the chance of an event happening and is equal to the number of favorable events divided by the total number of events. 
 The conditional probability predicts the happening of one event based on the happening of another event. Probability of an event = number of favorable outcomes/ sample space, Probability of getting number 10 = 3/36 =1/12. Calculate the probability of getting the sum of the numbers on the two dice is 6. Answer: Therefore the probability of getting a sum of 10 is 1/12. Answer: Therefore the probability of drawing a blue ball is 3/7. A probability is generally calculated for an event (x) within the sample space. The probability of any event depends upon the number of favorable outcomes and the total outcomes. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked. Any two mutually exclusive events cannot occur simultaneously, while the union of events says only one of them can occur. Probability Function: The function helps in obtaining the probability of every outcome. The prediction of the price of a stock, or the performance of a team in cricket requires the use of probability concepts. Outcome: The result of an event after experimenting with the side of the coin after flipping, the number appearing on dice after rolling and a card is drawn out from a pack of well-shuffled cards, etc. For any event the probability lies between 0 to 1. Example 01: Probability of obtaining an odd number on rolling dice for once. So for the probability that event A can happen, we are going to write P(A) and for the probability that event B can happen, we can write P(B). CBSE Previous Year Question Paper for Class 10, CBSE Previous Year Question Paper for Class 12. The theoretical probability calculates the probability based on formulas and input values. The formulas are based on these events only. Experimental probability is defined as the ratio of the total number of times an event has occurred to the total number of trials conducted. Solution: Sample Space = {1, 2, 3, 4, 5, 6}, P(Getting an odd number) = 3 / 6 = = 0.5. Some probability important formulas based on them are as follows: Example 01: Two dice are rolled simultaneously. Ph.D. vs. Master's Degree: What's the Difference? Statistics helps in rightly analyzing. Can I download the important notes on probability formula for free? 4. But for calculating probabilities involving numerous events and to manage huge data relating to those events we need the help of statistics. There are a few crucial terminologies that are associated with all probability formulas. n(B) is the number of favorable outcomes of an event 'B'. This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.
The conditional probability predicts the happening of one event based on the happening of another event. Probability of an event = number of favorable outcomes/ sample space, Probability of getting number 10 = 3/36 =1/12. Calculate the probability of getting the sum of the numbers on the two dice is 6. Answer: Therefore the probability of getting a sum of 10 is 1/12. Answer: Therefore the probability of drawing a blue ball is 3/7. A probability is generally calculated for an event (x) within the sample space. The probability of any event depends upon the number of favorable outcomes and the total outcomes. If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked. Any two mutually exclusive events cannot occur simultaneously, while the union of events says only one of them can occur. Probability Function: The function helps in obtaining the probability of every outcome. The prediction of the price of a stock, or the performance of a team in cricket requires the use of probability concepts. Outcome: The result of an event after experimenting with the side of the coin after flipping, the number appearing on dice after rolling and a card is drawn out from a pack of well-shuffled cards, etc. For any event the probability lies between 0 to 1. Example 01: Probability of obtaining an odd number on rolling dice for once. So for the probability that event A can happen, we are going to write P(A) and for the probability that event B can happen, we can write P(B). CBSE Previous Year Question Paper for Class 10, CBSE Previous Year Question Paper for Class 12. The theoretical probability calculates the probability based on formulas and input values. The formulas are based on these events only. Experimental probability is defined as the ratio of the total number of times an event has occurred to the total number of trials conducted. Solution: Sample Space = {1, 2, 3, 4, 5, 6}, P(Getting an odd number) = 3 / 6 = = 0.5. Some probability important formulas based on them are as follows: Example 01: Two dice are rolled simultaneously. Ph.D. vs. Master's Degree: What's the Difference? Statistics helps in rightly analyzing. Can I download the important notes on probability formula for free? 4. But for calculating probabilities involving numerous events and to manage huge data relating to those events we need the help of statistics. There are a few crucial terminologies that are associated with all probability formulas. n(B) is the number of favorable outcomes of an event 'B'. This formula is the number of favourable outcomes to the total number of all the possible outcomes that we have already decided in the Sample Space.